MEDIA ARITMÉTICA :
la media aritmética, también llamada promedio o media, de un conjunto finito de números es el valor característico de una serie de datos cuantitativos, objeto de estudio que parte del principio de la esperanza matemática o valor esperado, se obtiene a partir de la suma de todos sus valores dividida entre el número de sumandos. Cuando el conjunto es una muestra aleatoria recibe el nombre de media muestral siendo uno de los principales estadísticas muestrales .
Dados los n números la media aritmética se define como:
PROPIEDADES :
A) la suma de las desviaciones con respecto a la media aritmética es cero (0).
B) La media aritmética de los cuadrados de las desviaciones de los valores de la variable con respecto a una constante cualquiera se hace mínima cuando dicha constante coincide con la media aritmetica .
C) Si a todos los valores de la variable se le suma una misma cantidad, la media aritmética queda aumentada en dicha cantidad .
D) Si todos los valores de la variable se multiplican por una misma constante la media aritmética queda multiplicada por dicha constante .
E) Si media aritmética de un conjunto de números positivos siempre es igual o superior a la media geométrica .
EJEMPLO 01 :
En el experimento anterior, hemos tomado la primera muestra de manera errónea dándonos un resultado de 16. Calcular cómo varía la media aritmética: Muestras: 16 , 11, 10, 9, 10, 10
Número de muestras: 6
Media Aritmética: (16 + 11 + 10 + 9 + 10 + 10) / 6 = 66 / 6 = 11 → vemos que la media aritmética aumenta en valor de 1 al tomar el valor erróneo.
EJEMPLO 02 :
Considérense los siguientes datos: 3, 8, 4, 10, 6, 2. Se pide:
1. Calcular su media.
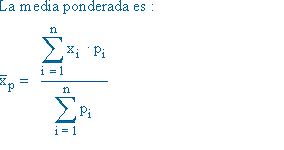
LA MEDIA PONDERADA :
La media ponderada es una medida de tendencia central, que es apropiada cuando en un conjunto de datos cada uno de ellos tiene una importancia relativa (o peso) respecto de los demás datos. Se obtiene multiplicando cada uno de los datos por su ponderación (peso) para luego sumarlos, obteniendo así una suma ponderada; después se divide esta entre la suma de los pesos, dando como resultado la media ponderada :
La media aritmética está comprendida entre el valor máximo y el valor mínimo del conjunto de datos:
EJEMPLO 01 :
Se puede usar una media ponderada para calcular la nota final de un curso escolar, en donde se asigna distinta importancia (peso) a los distintos exámenes que se realicen. Por ejemplo, los dos primeros exámenes tienen un peso o valor de 30% y 20% respectivamente, y el último del 50%; las calificaciones respectivas son de 6.4, 9.2 y 8.1, entonces la nota final corresponde a la siguiente media ponderada:
EJERCICIO 02 :
Tomamos cuatro elementos evaluables y calculamos la nota final de una asignatura usando la media ponderada de las notas que han obtenido el alumno. Damos diferentes pesos según la importancia de la siguiente forma: un peso de 3 al examen inicial, de 1 al trabajo entregable, 2 al trabajo final y 4 al examen final. En la tabla siguiente se muestra las notas de un alumno y sus pesos:
MEDIA GEOMÉTRICA :
En MATEMATICAS y ESTADISTICA , la media geométrica de una cantidad arbitraria de números (por decir n números) es la RAIZ ENESIMA del producto de todos los números; es recomendada para datos de progresión geométrica, para promediar razones, interés compuesto y números índices.
EJEMPLO 01 :
Una cadena de expendedores de gasolina el año pasado aumentó sus ingresos respecto al año anterior en 21%; y han proyectado que este año van a llegar a un aumento de 28% con respecto al año pasado. ¿Cuánto es el promedio anual del aumento porcentual?
Definitivamente no es (21% + 28%):2 = 24,5%.
EJEMPLO 02 :
En una empresa quieren saber la proporción media de mujeres en los diferentes departamentos. Para ello, se recoge el porcentaje de mujeres en los cinco principales departamentos.
MEDIA ARMÓNICA:
La media armónica (designada usualmente mediante H) de una cantidad finita de números es igual al reciproco , o inverso, de la media aritmética de los recíprocos de dichos valores y es recomendada para promediar velocidades.
Así, dados n números x1, x2, ... , xn la media armónica será igual a:
La media armónica resulta poco influida por la existencia de determinados valores mucho más grandes que el conjunto de los otros, siendo en cambio sensible a valores mucho más pequeños que el conjunto.
La media armónica no está definida en el caso de que exista algún valor nulo.
PROPIEDADES:
La inversa de la media armónica es la media aritmética de los inversos de los valores de la variable.
Siempre se puede pasar de una media armónica a una media aritmética transformando adecuadamente los datos.
La media armónica siempre es menor o igual que la media aritmética, ya que para cualquier número real positivo.
EJEMPLO 01:
Supongase que una familia realiza un viaje en automóvil a un ciudad y cubre los primeros 100 km a 60 km/h, los siguientes 100 km a 70 km/h y los últimos 100 km a 80 km/h. Calcular, en esas condiciones, la velocidad media realizada.
EJEMPLOS 02 :
Un tren realiza un trayecto de 400km. La vía tiene en mal estado que no permitían correr. Los primeros 100 km los recorre a 120km/h, los siguientes 100km la vía está en mal estado y va a 20km/h, los terceros a 100km/h y los 100 últimos a 130km/h. Para calcular el promedio de velocidades, calculamos la media armónica.
.jpg)